我們昨天簡單地提到了線性回歸，也實際以視覺化的方式去呈現最簡單的線性回歸的案例，在給定訓練資料後，可以有方法讓機器去找到最接近的函式。
今天要更詳細地去了解整個過程！

Linear Regression 詳細流程－依JOHN國為例

首先，再次把昨天的JOHN國召喚出來(也就是我們的訓練資料們)：
id | price | sqft_living
------------- | ----------
1 | 500000 | 55
2 | 275000 | 27
3 | 360000 | 33
4 | 780000 | 70
5 | 145000 | 13
6 | 280000 | 26
7 | 860000 | 89
8 | 200000 | 21
9 | 90000 | 10
10 | 680000 | 67

在【Day 03】我們的起點：機器學習介紹（2/2）有提到超級簡化的機器學習流程，而Linear Regression也是機器學習的一種，所以在流程上面大致相同。

超級簡化的流程：

1. 訂出函式池子
2. 判定函式的好壞
3. 挑出最好的函式

有了超級簡化步驟，又有訓練資料，你還等什麼，開始拉！

第一步：訂出函式池子

我們假設JOHN國的房價只受到坪數影響，所以這裡會直覺地假設price和sqft_living的關係是很簡單的方程式 y = w * x + b，當然此時的y會是price，而x會是sqft_living。而我們相信有存在一組最適當的w和b來表示price和sqft_living之間的關係，所以我們的目標就是要找出w和b。

補充1：w稱為權重(weight)，b叫做偏差(bias)
補充2：因為是"Linear" Regression，所以當輸入的x很多(例如影響房價的因素除了坪數之外，還有廁所幾個、停車場幾個等等)，所以當有很多x(因素)時，方程式可以簡化寫成下列方程式(i代表不同的w和x的編號)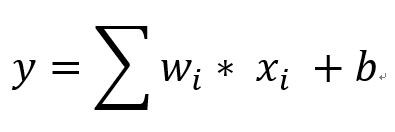

當我們訂下y = w * x + b，將會有無限多個方程式(也就是我們的函式池子)，如以下
y = 500 * x + 200
y = -100 * x + 800
y = 0.5 * x + 20
等等．．．

第二步：判定函式的好壞

我們有提到第二步是要判定函式的好壞，但實際上要怎麼做呢？這裡要先提到一個新的名詞叫做損失函式(Loss function)，那損失函式要幹嘛呢?它要用來協助我們判定一個方程式的好壞。

補充：損失函式也可以說是函式的函式，它的input是函式池子裡的函式，而它會output出這個函式到底多好多不好。

第三步：挑出最好的函式

終於到最後一步，就是我們要想辦法找到一個F讓損失函數最小(為什麼要最小明天會提到)，這樣就是我們要的最好函式F了！所以我們可以開始代所有的在函式池子裡的函式(也就是各種w和b)，然後終究會找到一組w和b使得損失函數會是最小的。
但這樣實在是太沒有效率了(因為有無窮個)，這時候我們會用一個方法，叫做梯度下降法(Gradient Descent)，它會協助我們持續逼近最好的w和b。

今天比較詳細地提及整個Linear Regression的流程，讓大家更好理解整個過程，同時也帶出其中的兩個重要的方程式－Loss fuction和Gradient Descent。

明天會開始介紹這兩個方程式，是很吃重數學的地方，也是相對較難理解的地方，我會盡量以白話的口吻分享它們！加油！